Tételezzük fel, hogy a munkahelyi vezetőnk arra kért minket, jósoljuk meg a vállalat következő évi árbevételét. Ehhez rengeteg adat áll rendelkezésünkre, de nem tudjuk, hogy melyek azok, amelyek valóban hatással vannak az árbevételre és melyek azok, amelyeket érdemes figyelmen kívül hagynunk. Ilyen és ehhez hasonló kérdések megválaszolásához alkalmazhatunk regresszióelemzést.

A prediktív analitikai elemzések és – így a regresszióelemzés is – egyre fontosabb információkat szolgáltatnak nem csak az értékesítés és a marketing számára, de a controlling területnek is. Nagyvállalati környezetben ezeket az elemzéseket sokszor olyan robosztus rendszerek támogatják, amelyeket a kis- és középvállalkozásoknak nem éri meg kialakítani és fenntartani. Egyszerűbb regressziós elemzéseket azonban Excel segítségével is elvégezhetünk. Ez nem csak a meglévő adataink közti összefüggések megértésében nyújthat segítséget, hanem kiválóan alkalmazható előrejelzések készítésére is.

Mi az a lineáris regresszió, hogyan számoljuk?

A regresszió két vagy több változó közti kapcsolat elemzésének elterjedt eszköze. Alapesetben azt vizsgálja, hogy egy kitüntetett – a vizsgálat tárgyát képező – változó hogyan függ egy vagy több úgynevezett magyarázó (másnéven független) változótól. Amennyiben egyetlen magyarázó változónk van, egyváltozós regresszióról beszélünk, egynél több változó esetén pedig többváltozós regresszióról.

Lineáris regresszió alkalmazása során az úgynevezett függő változó változásait próbáljuk magyarázni a független változók segítségével. Formálisan:

y=a+b*X+ε, ahol

y = függő változó

a = tengelymetszet

X = független változók együttese

b = független változók együtthatói (koefficiensek)

ε = hibatag, amely a függő változó tényleges értéke és a becsült értéke közötti különbség

A képlettől nem kell megijednünk, egy gyakorlati példára fordítva könnyen megérthetjük azt. Például ha egy adott hónapban eladott esernyők száma (függő változó) és az adott hónapban leesett csapadékmennyiség (független változó) közti kapcsolatot vizsgáljuk, akkor ezt a fenti képlet segítségével lineáris regresszió alkalmazásával a következőképp írhatjuk le:

• Eladott esernyők száma = a + b * leesett csapadék mennyiség + ε

Ebben az esetben egy egyváltozós (leesett csapadék mennyisége) regressziót alkalmaznánk. A képlet egyes változóiról a későbbiekben még ejtünk szót, ezzel tovább segítve a megértést.

Hogyan végezzünk regressziószámítást Excelben?

Előkészületek I. – Adatelemzési bővítmény engedélyezése

A regressziószámítás első lépéseként győződjünk meg arról, hogy az Excelünkben engedélyezve van a „Data Analysis ToolPak” nevű bővítmény. Ezt könnyedén megtehetjük az alábbi módon:

1. Kattintsunk az Excelben a menüsoron a Fájl menüpontra, majd kattintsunk a Beállítások opcióra
2. A felugró ablakon kattintsunk a Bővítményekre, majd az Ugrás gombra (figyeljünk, hogy a Kezelés ablakban az „Excel-bővítmények” legyenek kijelölve)

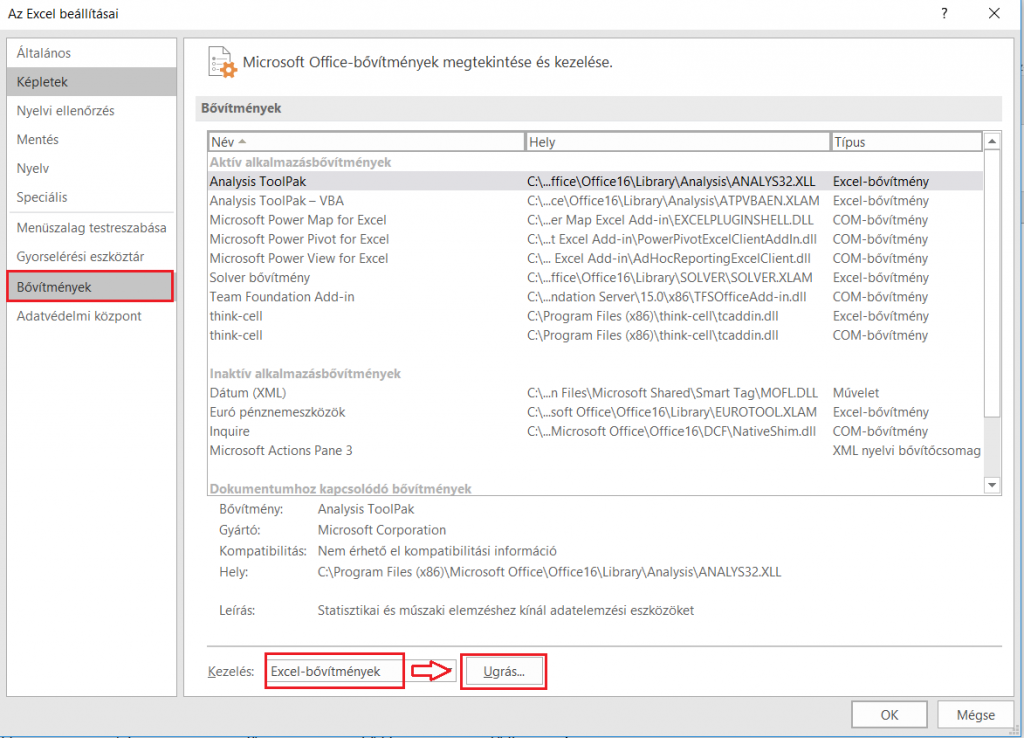
3. Végezetül a Bővítménykezelő ablakban tegyünk egy pipát az „Analysis ToolPak” mellé, majd nyomjuk meg az Ok Ha mindent jól csináltunk, akkor az Adatok fülön megjelenik az „Adatelemzés” nevű eszköz.

Előkészületek II. – Kiindulási adathalmaz összeállítása

A lineáris regresszió elvégzéséhez a következő lépésben össze kell állítanunk egy olyan kiindulási adattáblát, amelyben a vizsgálni kívánt függő és független változóink vannak. Ahhoz, hogy az Excel beépített eszközével el tudjuk végezni a regressziószámítást, fontos, hogy a változóinkat külön oszlopokban és ne sorokban vegyük fel. A következőkben egy konkrét példán keresztül mutatjuk be a regressziószámítás menetét.

A regressziószámítás menete

Az alábbi példában egy képzeletbeli vállalat adatait fogjuk elemezni. A kijelölt függő változónk (amelynek az értékét előre szeretnénk jelezni) a cég árbevétele lesz, független változóként pedig négy változót adtunk meg: a cégnél dolgozók létszámát, a cégben futó projektek számát, a cég honlapjának látógatói számát és a céghez beérkező hívások számát. A számításhoz használt példatáblánk struktúrája a következő:

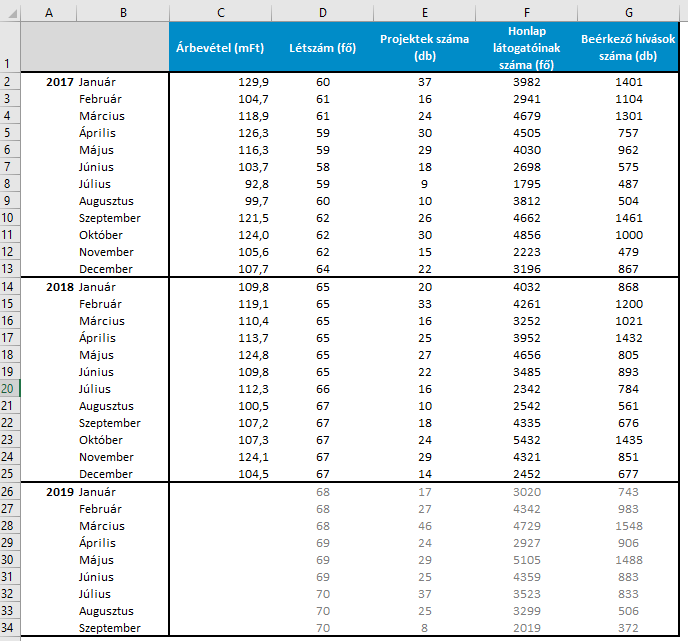
A táblázatunkon látjuk, hogy rendelkezésünkre állnak a 2017-es és 2018-as árbevétel adatok, valamint a független változóink. A következőkben a független változók becsült 2019-es értékei alapján (a táblázatunkban világosszürke értékek) azt szeretnénk kiszámítani, hogy 2019 első kilenc hónapja során milyen árbevételre számíthatunk. Ehhez először regresszióanalízist kell végeznünk, hogy megállapítsuk, milyen mértékben és hogyan magyarázzák a független változóink az árbevételünket.

A regressziószámítás első lépéseként kattintsunk az Adatok fülön az előkészületek során engedélyezett Adatelemzés gombra, majd az itt megjelenő ablakon válasszuk ki a „Regresszió” opciót. Az így felugró ablakban adjuk meg a következő beállításokat:

1. Bemeneti Y tartománynak adjuk meg a függő változónk (árbevétel) 2017-es és 2018-as értékeit (ebben az esetben C2:C25).
2. Bemeneti X tartományként pedig válasszuk ki a független változóink értékeit (ebben az esetben D2:G25). Fontos, hogy az X tartomány így megadott oszlopainak közvetlenül egymás mellett kell elhelyezkedniük.
3. A „Feliratok” mellé akkor tegyünk pipát, ha a fejléceket is kijelöltük. Esetünkben a megadott tartományok nem tartalmazzák a fejléceket, ezért ezt üresen hagyjuk.
4. A Kimeneti beállításoknál kiválaszthatjuk, hogy hová szeretnénk az eredményünket elhelyezni (ajánlott külön munkalapra).
5. Opcionálisan jelöljük be a „Maradékok” jelölőnégyzetet, ha látni akarjuk, hogy mennyire térnek el a becsült és a tényleges árbevétel értékeink.

6. Végezzük el a számításunkat az OK gombra kattintva!

Az eredmények kiértékelése

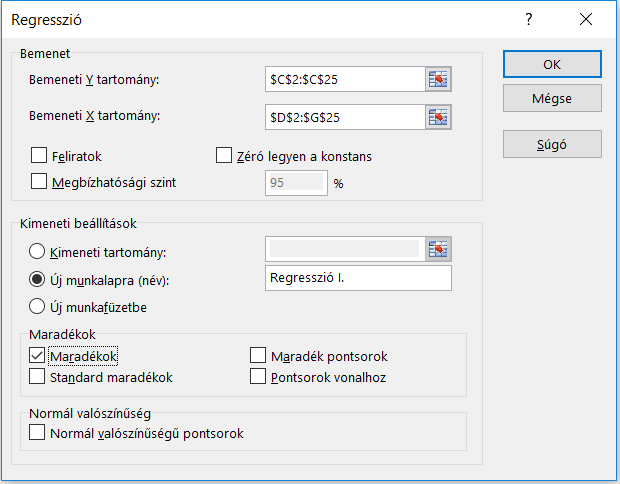
Az eredményül kapott új munkalap sokakat elrémíthet, de a következőkben segítünk értelmezni, hogy mit is jelentenek a legfontosabb értékek.

1. Összesítő tábla

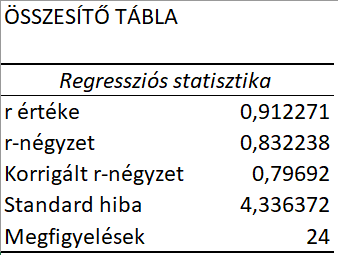
Itt alapvetően két dolgot érdemes most vizsgálnunk:

r értéke: R-nek nevezzük azt a korrelációs együtthatót, amely két változó közötti lineáris kapcsolat erejét méri.* A korrelációs együttható bármely érték lehet -1 és 1 között, abszolút értéke pedig a kapcsolat erejét jelzi. Minél nagyobb az abszolút érték, annál erősebb a kapcsolat:

• Az 1 erős pozitív kapcsolatot jelent (az egyik változó növekedése a másik változó növekedésével jár együtt)
• -1 erős negatív kapcsolatot jelent (az egyik változó növekedése a másik változó csökkenésével jár együtt)
• 0 egyáltalán nem jelent lineáris kapcsolatot

r-négyzet: az r-négyzet egyszerűen az előző R korrelációs együttható négyzete, amelyet a modell magyarázó erejének mérésére alkalmazunk. Minél közelebb van 1-hez, annál jobban magyarázzák a független változók a függő változó értékeit. Az, hogy mekkora R² érték jelent jó magyarázó erőt, modellről modellre eltér, de általában 0,7 feletti értékek már erős kapcsolatot mutatnak.

Példánkban az R² = 0.83 (két számjegyre kerekítve), ami azt mutatja, hogy a független változóink jól magyarázzák a függő változót, esetünkben az árbevételt. Más szóval a függő változó viselkedésének 83%-át magyarázhatjuk a független változók segítségével.

2. Együtthatók táblája

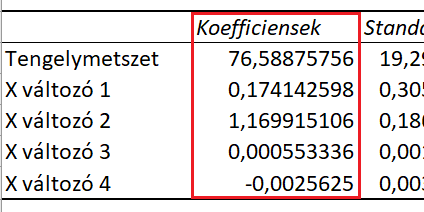
Ha visszaemlékezünk a lineáris regresszió képletére (y=a+b*X+ε), akkor a képletet alkalmazva esetünkben a következő összefüggést írhatjuk fel az árbevételre vonatkozóan:

Árbevétel = 76,589 + 0,174 * Létszám + 1,17 * Projektek száma + 0,0006 * Honlap látogatóinak száma – 0,0026 * Beérkező hívások száma

A magyarázó változó pozitív együtthatója azt jelenti, hogy a magyarázó változó növekedése esetén a függő változó is növekszik, negatív értéknél pedig csökken. Esetünkben a létszám, a projektek száma és a honlap látogatószámának növekedése pozitívan hat az árbevételre, míg a bejövő hívások számának növekedése minimálisan, de csökkentik azt. Magyarázat lehet erre, ha az ügyfelek a panaszukkal kapcsolatban telefonálnak, vagy ha a vállalatnak többe kerül a hívásokat kiszolgálni, mint amennyi árbevételt ezekből generálni tud.

Árbevétel előrejelzése és záró gondolatok

A fenti összefüggés birtokában már képesek vagyunk előre jelezni a cég árbevételét a független változók becsült értékei alapján, ha a 2019-es év egyes hónapjaira alkalmazzuk a képletünket:

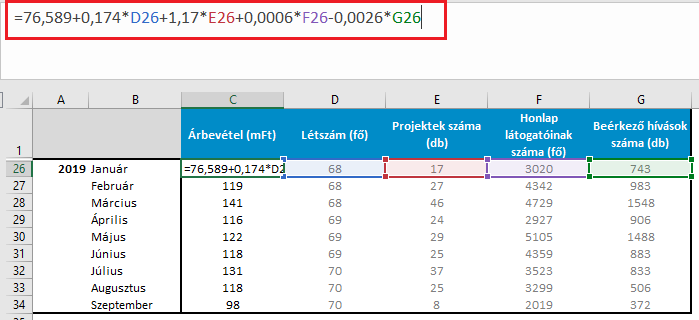
Fontos, hogy a bemutatott példa a megértés könnyítése érdekében sok helyen él egyszerűsítésekkel. Megbízható regressziós modellek készítéséhez például a kiindulási adathalmaznak több feltételnek is meg kell felelnie, valamint a valóságban a független változóinkat is pontatlanul tudjuk csak előre megbecsülni. A regressziószámítás eredményeit ezért fenntartásokkal kell kezelnünk, és csak körültekintő statisztikai tesztek elvégzése után győződhetünk meg az eredmények relevanciájáról. Semmiképpen nem javasoljuk tehát, hogy csupán a cikkben bemutatott példára alapozva hozzunk üzleti döntéseket, azonban a regressziós elemzés még így is hasznos eszköz arra, hogy jobban megértsük az adataink közti kapcsolatokat és összefüggéseket.

* A korrelációs együtthatóra leggyakrabban nagy R betűvel hivatkozunk, de az Excel kis r-ként tünteti fel.

Források:

Christian Langmann: Predictive Analytics für Controller – einfache Anwendungen mit MS Excel, Controller Magazin 2018/4

https://www.ablebits.com/office-addins-blog/2018/08/01/linear-regression-analysis-excel/